GRAFIS AIDS UNTUK PERHITUNGAN SALURAN TRANSMISI

beli domain indonesia, biaya kuliah universitas pancasila, biaya kuliah universitas trisakti, Blok Mesin, cloud hosting indonesia, cloud server indonesia, daftar universitas di indonesia, Danareksa Online Trading, dedicated server indonesia, Desain Mesin, domain dan hosting, domain dan hosting adalah, domain hosting murah, domain murah, domain paling murah, download software pc terbaru, file hosting indonesia, Gambar Mesin, Gambar Mesin Bubut, harga hosting website, harga web hosting, host indonesia, Hosting And Domain, hosting domain, hosting domain murah, Hosting Web, Info Mesin, Jasa Pembuatan Website Iklan Baris, jurusan universitas indonesia, Keamanan Sistem Informasi, Kumpulan Software Komputer, Mesin 4 Tak, Mesin Ayakan Pasir, Mesin Ball Mill, Mesin Blow Moulding, Mesin Briket, Mesin Bubut Universal, Mesin Crusher Batu, Mesin Crusher Plastik, Mesin Genteng, Mesin Giling Cabe, Mesin Giling Ikan, Mesin Giling Kedelai, Mesin Grinder, Mesin Hammer Mill, Mesin Kompos, Mesin Korter, Mesin Mie, Mesin Miling, Mesin Milling Vertikal, Mesin Obras, Mesin Offset Printing, Mesin Pembuat Bakso Ikan, Mesin Pencacah Rumput, Mesin Pendulang Emas, Mesin Penepung, Mesin Pengayak Pasir, Mesin Penggiling Mie, Mesin Penghancur Kayu, Mesin Pengolahan Karet, Mesin Penyedot Pasir, Mesin Perontok Padi, Mesin Pertambangan Emas, Mesin Pertukangan, Mesin Press Hose, Mesin Roll Forming, Mesin Rotary Dryer, Mesin Sedot Pasir, Mesin Serut, Mesin Spray Dryer, Mesin Stone Crusher, Mesin Tahu, Mesin Tepung, Mesin Tusuk Gigi, Mesin Tusuk Sate, Model Baju Bunga, Sistem Basis Data, Sistem Multimedia, Software Untuk Mengakses Internet, Spesifikasi Komputer Server, universitas internasional batam, universitas islam attahiriyah, universitas multimedia nusantara, universitas pendidikan indonesia, usaha kesehatan sekolah, vps indonesia, web hosting gratisan, web hosting indonesia, web hosting support php, Web Hosting Terbaik Di Indonesia, Web Hosting Terbaik Indonesia, web hosting termurah, Webhost Indonesia, webhosting indonesia, webhosting terbaik, website builder indonesia

Bagan Smith. Diamete.r pusat vertikal dari grafik adalah koordinat lz, .I = 1, yaitu lokus dari semua impedansi dari kesatuan besarnya yang dinormalisasi. Dua impedansi dari sudut fasa yang sama tetapi dengan besaran normalisasi terkait timbal balik terletak pada titik-titik bayangan-cermin relatif terhadap diameter vertikal pusat ini.

Gambar 9-15. Grafik Carter. Koordinat dari besaran impedansi ternormalisasi dan sudut fasa pada bidang koefisien refleksi.

Gbr.9-14. Menentukan impedansi dari kesatuan besarnya yang dinormalisasi yang akan menghasilkan VSWR sebesar 3,00.

Gambar 9-15.Gunakan diagram Smith untuk menentukan impedansi yang dinormalisasi transformasi antara dua lokasi pada misi trans lossy baris.

Pada Gambar 9-15, r ,. dan x,. adalah komponen ized yang normal dari impedansi pada beberapa koordinat d pada saluran transmisi yang memiliki faktor atenuasi yang terbatas. Diharapkan untuk mengetahui komponen impedansi ternormalisasi r dan x pada titik d1 pada garis, d1 berada di sisi sumber sinyal dari d. Dari persamaan (9.18) koefisien refleksi pada koordi nate d1 akan memiliki sudut fasa yang lebih kecil dengan 2, B (d1 - d) = (4r./.\)(d1-d) daripada sudut fasa koefisien pantulan di koordi nate d. Impedansi ternormalisasi pada titik d1 karena itu akan berada pada radius grafik yang terletak searah jarum jam (menurun <f>) dari lokasi sudut dari impedansi ternormalisasi pada d, dengan sudut dalam radian yang adalah.4 ,, - kali panjang saluran transmisi dalam panjang gelombang antara dua titik. Skala sudut pada grafik yang akan digunakan untuk menentukan transformasi impedansi antara dua lokasi pada saluran transmisi karena itu harus skala lin.lar pada tingkat. dari 2 ,,. radian (satu rotasi penuh) di sekitar grafik untuk setiap setengah panjang gelombang. Skala sudut terluar pada diagram Smith pada Gambar 9-3 adalah skala seperti itu, dan tulisan WAVELENGTHS TOWARD GENERATOR menunjukkan bahwa transformasi dari koordinat d ke koordinat d1 searah jarum jam pada skala ini jika d1 lebih dekat ke sumber sinyal atau generator dari d adalah. Dipasangkan dengan skala di atas dan hanya di dalamnya, adalah skala identik yang meningkat dalam arah berlawanan arah jarum jam dan diberi label WAVELENGTHS TOWARD LOAD untuk transformasi dari d ke d1 ketika d1 berada di sisi beban terminal d. Untuk masalah transformasi ini, fakta bahwa asal untuk kedua skala koordinat sudut adalah pada sumbu horizontal tangan kiri tidak memiliki arti. The Smith chart "slide rule" yang disebutkan dalam Bagian 9.4 memungkinkan rotasi skala koordinat sudut relatif terhadap badan utama grafik, sehingga asal skala ini dapat diatur pada titik yang diinginkan.

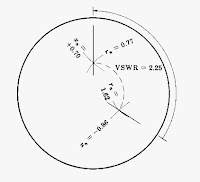
Untuk menghitung impedansi ternormalisasi pada konektor, nilai VSWR = 2,26 dan dvcm1n /> .. 0,180 / 0,900 = 0,200 digunakan. Hasilnya adalah r,. +; .. = 1,62 -; o.86, menggunakan metode Contoh 9.4. Lokasi titik pada diagram Smith ditunjukkan pada Gambar 9-16. Nilai Thia dari r,. +; .. adalah impedansi masukan yang dinormalisasi dari saluran transmisi, yang panjang gelombangnya adalah 4 .17. Impedansi beban terminal yang dinormalisasi terhubung ke garis karena itu ditemukan dengan bergerak 0,17 WAVE LENGTHS TOWARD LOAD, yaitu. berlawanan arah jarum jam, di sepanjang lingkaran VSWR konstan melalui titik impedansi input yang dinormalisasi. Panjang gelombang 4,00 dari panjang garis transmiasi tidak berpengaruh pada hasil, karena mereka hanya mewakili delapan rotasi lengkap di sekitar grafik kembali ke titik awal. Impedansi dinormalkan antena sebagai impedansi beban terminal, ditemukan menjadi 0,77 +; 0,70; dan impedansi adalah (0,77 +; 0,70) (60 +; o) = 87,6 + j86 ohm. Frekuensi pengukuran adalah 3,00 X 108 / 0,900 = 333 megahertz

Karena bagian slotted dan saluran transmisi dalam masalah ini memiliki impedansi karakteristik yang sama, kecepatan fase yang sama, dan atenuasi yang sama (nol), itu sebenarnya tidak diperlukan untuk menghitung impedansi pada konektor sebagai langkah menengah. Jika bagian slotted dan jalur transmiaaion dianggap sebagai satu kesatuan sistem uniform yang terus menerus, impedansi antena beban terminal dapat dievaluasi secara langsung dari fakta bahwa ia menghasilkan VSWR sebesar 2,26 dan dv <mln> /> .. dari 0,20 + 4,17 = 4,37.

Gambar 9-16. Menormalkan transformasi impedansi ke arah beban pada garis tranamlasion loaaless.

Gambar 9-17. Menentukan faktor atenuasi dan kecepatan fase dari garis tranamiuion dari impedansi input yang tidak dinormalisasi dari bagian garis dengan terminasi hubung singkat.

Suatu bagian jalur transmisi frekuensi tinggi koaksial plastik-dielektrik yang fleksibel adalah 24,26 m panjang. Pada frekuensi 60,0 megahertz, impedansi karakteristik i172 +; o ohm, dan input i_mpedance dari bagian i1 diukur menjadi 106 +; 122 ohma pada frekuensi tersebut ketika ujung terminal-beban dari bagian

Persamaan (ɡ_n, + jb_n) = 1 (r_n + jx_n) = r_nl (r²_n+ x²_n) - jx_n(r²_n+ x²_n) menunjukkan bahwa tanda b_n selalu berlawanan dengan x_n . Bagian atas bagan Smith berisi semua impedansi normalisasi yang x_n adalah positif, atau admitansi normalisasi yang b_n adalah negatif. Di bagian bawah grafik, tanda-tanda dibalik.

Gambar 9-19. Grafik Smith dengan konduktansi normal dan koordinat dugaan pada bidang koefisien refleksi

Dalam kasus saluran transmisi, ketika bagian saluran transmisi yang berbeda terhubung bersama dalam sistem multi-cabang, mereka hampir selalu terhubung secara paralel pada persimpangan (Gambar 9-20 (a)) daripada seri (Gambar. 9 -20 (b)), untuk alasan yang mungkin sebagian listrik dan sebagian mekanis.

Gbr.9-24. Saluran transmisi cabang yang terhubung (a) secara paralel dan (b) secara seri dengan saluran transmisi utama.

Gambar 9-22. Penentuan beban masuk terminal yang dinormalisasi dari data gelombang berdiri pada garis lossless.

Sama seperti bagan Carter dari Bagian 9.5 dan Gambar 9-13 disajikan koordinat magnitudo dan sudut fasa dari impedansi ternormalisasi pada bidang refleksi ko-efisien, sehingga koordinat yang sama diputar 180° pada bidang menjadi koordinat magnitudo dan sudut fasa dari masuk dinormalisasi, seperti ditunjukkan pada Gambar. 9-24. Gambar 9-24 diperoleh dari Gambar 9-13 dengan mengubah tanda koordinat sudut fase dan mengubah nilai pada setiap koordinat besarnya yang dinormalkan menjadi timbal balik.

Gambar 9-23. Penentuan susunan yang dinormalisasi dari bagian garis lossless dengan penghentian sirkuit pendek.

Gambar 9-24. Grafik Carter dengan koordinat magnitudo dan sudut fasa dari penerimaan yang dinormalisasi

9.9 Penggunaan matematis lainnya dari grafik smith

Dari derivasi yang diberikan sebelumnya dalam bab ini dan dalam bab 7, prosedur grafis yang cukup sederhana memungkinkan untuk menggunakan diagram smith untuk mengevaluasi tangen hiperbolik yang empuk dan cotangents tan x dan cot x. Ini juga dapat digunakan untuk mengevaluasi bilangan eksponensial kompleks, e^{± (x + jy)}, dan dengan ekstensi sinh (x + jy) dan cosh (x + jy).

Demonstrasi penggunaan dari untuk beberapa tujuan ini ditugaskan sebagai masalah di bawah ini.

9.10 Pengembalian kerugian, kehilangan refleksi, dan kehilangan transmisi.

Demonstrasi penggunaan dari untuk beberapa tujuan ini ditugaskan sebagai masalah di bawah ini.

9.10 Pengembalian kerugian, kehilangan refleksi, dan kehilangan transmisi.

Konsep "return loss" adalah sederhana dan mudah.Pada titik tertentu pada saluran transmisi uniorm daya yang dibawa oleh gelombang yang dipantulkan (perjalanan dari beban terminal menuju sinyal sumber) akan kurang dari daya yang dibawa oleh gelombang insiden (perjalanan dari sumber sinyal menuju beban terminal) ketika besarnya koefisien refleksi pada beban terminal dan garis adalah lss daripada kesatuan, atau ketika ada redaman antara titik spesifik dan beban terminal . Nilai dari return loss pada suatu titik pada suatu sistem berguna sebagai indikasi sejauh mana pantulan gelombang saya menurunkan pengoperasian sistem pada titik tersebut. Degradasi seperti itu dapat mengakibatkan, misalnya, dari gelombang yang dipantulkan menjadi sinyal gema yang mengganggu, atau dari yang mempengaruhi frekuensi atau output daya dari sumber sinyal dengan menyebabkan impedansi input dari garis. Spesifikasi desain untuk beberapa bentuk sirkuit komunikasi saluran transmisi dapat menyatakan nilai minimum return loss yang harus dipertahankan atas beberapa bagian dari sistem.

Konsep ini langsung berlaku hanya untuk sirkuit saluran transmisi dari bentuk yang ditunjukkan pada Gambar 9-26. di mana impedansi sumber sama dengan impedansi karakteristik dari garis. Garis mungkin memiliki nilai total redaman asalkan redaman per panjang gelombang cukup kecil untuk memastikan bahwa impedansi karakteristik memiliki sudut fase yang dapat diabaikan.

Gambar 9-26. Sirkuit saluran transmisi di mana grafik "Reflection Loss" radial smith chart berlaku.

Analisis berikut menegaskan bahwa pengurangan daya ditunjukkan terjadi, dan menunjukkan selain itu adalah garis memiliki total redaman total (tetapi impedansi karakteristik nyata) pengurangan daya yang disampaikan oleh sumber tidak mencerminkan ke garis, ketika impedansi beban terminal adalah berubah dari tidak reflektif ke mencerminkan, sama dengan kekuatan dalam gelombang yang dipantulkan pada titik refleksi kurang kekuatan yang hilang oleh gelombang yang dipantulkan di atenuasi garis.

Menerapkan persamaan (7.1), (7.8) dan (7.8) ke sirkuit gambar. 9-26,

V (z = 0) = V_inp= V₁ + V₂ = V₁(1+_pt^-2yt)

I (z = 0) = I_inp= (V₁/ Z₀) (1-_pt^e-2yt)

Tapi V_inp = Vs - I_inpZs = V_s - I_inpZ_o.Oleh karena itu V₁(1+_pt^e-2yt) = Vs -V₁(1-_pt^e-2yt), dan V₁= 1 / 2Vs, hasil yang bisa ditulis langsung dengan menggunakan analisis refleksi ganda dari bagian 8.8. Penting untuk dicatat bahwa pernyataan ini tidak sama dengan V_INP = 1/2 V_s,yang akan menjadi benar hanya jika Z_T= Z₀ dan _pt= 0.

Persamaan (9.17) dan (9.18) kemudian dapat ditulis ulang,

V_inp= 1/2 Vs (1+_pt^-2ytinp)

I₌1/2(V₁/ Z₀) (1-_pt^e-2yt)

Dari persamaan dengan persamaan (7.14), halaman 180.

Jika Z_T
=Z_0, _PT = 0. Kemudian input daya ke saluran adalah P_o = 1/4 | V_s|²/ Z_0,dan daya yang mencapai beban terminal adalah P₀e^-2al. Jika Z_T≠ Z₀, kekuatan dalam gelombang insiden awal mencapai beban terminal (yang merupakan titik refleksi adalah P₀e-^2al|_PT|², dan daya yang diterima oleh beban adalah P₀e^-2al( 1- |_PT|²⁾.

Jika saluran transmisi tidak lossless, konservasi energi menuntut bahwa kehadiran gelombang yang dipantulkan tunggal harus menyebabkan sumber memberikan daya yang lebih kecil untuk menjadi terminal input dari garis dengan tepat jumlah power dalam gelombang yang dipantulkan.

Analisis berikut menegaskan bahwa pengurangan yang ditunjukkan dalam daya memang terjadi, dan menunjukkan selain bahwa jika garis memiliki total attenuattion yang terbatas (tetapi impedansi karakteristik nyata) pengurangan daya yang disampaikan oleh nonreflecting ke nonreflecting, sama dengan kekuatan dalam Gelombang yang dipantulkan pada titik refleksi kurang kekuatan yang hilang oleh gelombang yang dipantulkan di atenuasi garis.

Persamaan Appliying (7.1), (7.3) dan (7.8) ke sirkuit Gambar. 9-26,

V (_z= 0) = V_inp = V₁+ V₂ = V₁+ V₂= V₁(1 + p_Te^-2yt)

I (z = 0) = I_inp = (V₁/ Z₀) (1-P_T^e-2YT)

Tetapi Vinp = V_S - I_inpZs = Vs-I_inpZ_o. Oleh karena itu V₁(1 + p_Te^-2yt) = Vs-V₁(1-_pTe^-2yt), dan V₁ = 1 / 2V_S, sebuah resut yang bisa saja ditulis secara langsung dengan menggunakan analisis refleksi berganda dari sectin 8.8 Penting untuk dicatat bahwa stetemen ini tidak setara dengan V_inp = 1 / 2Vs, yang akan benar hanya jika ZT = Z₀dan _PT= 0.

Ketika Z_T≠ Z_0,tetapi menghasilkan koefisien refleksi PT pada beban terminal, telah ditunjukkan di atas bahwa input daya untuk garis falss ke P₀(1- |_PT|²e^-4al),sedangkan kekuasaan disampaikan untuk beban menjadi P₀e^-2al(1- |_PT|²). Perbedaannya adalah P₀(1-e^-2al) (1+ |_PT|²e^-2al), yang merupakan daya yang hilang di saluran. Rasio daya yang hilang dalam kasus pertama adalah (1+ |_PT|²e^-2al).

Dalam menggunakan konsep refleksi loss dan koefisien loss transmisi untuk membuat perhitungan pada sirkuit saluran transmisi memiliki bentuk gambar. 9-26, dengan redaman garis yang terbatas, perawatan harus dilakukan untuk tidak menghitung komponen kerugian sebanyak dua kali. Ketika impedansi beban terminal Z_T diubah dari Z₀ ke beberapa nilai lainnya, tanpa mengubah V_S, telah terlihat bahwa beberapa perubahan dalam hubungan kekuasaan di sirkuit terjadi secara bersamaan: (a) gelombang pantulan dibuat, yang merupakan pengurangan tak terduga dalam daya yang dikirimkan ke beban terminal; (b) gelombang yang dipantulkan mengalami kehilangan daya disipasi pada pelemahan garis; (c) daya input ke saluran dikurangi; (D) kerugian atenuasi total dalam garis yang meningkat.

Koefisien refleksi beban terminal adalah 0,5 + j0, sehingga |_pT| = 0,5. Dari skala radial Gambar. 9-3, kehilangan pantulan ditemukan menjadi 1,25 db. Untuk rangkaian yang sama dengan Z_T = Z₀ = 50 + j0 ohm, daya input ke saluran ini mudah dihitung sebagai 0,500 watt, daya yang dikirimkan ke beban adalah 0,125 watt, dan daya yang didisipasikan di garis redaman adalah perbedaan, atau 0,375 watt. Dari definisi kehilangan refleksi, daya mencapai beban ketika Z_T = 150 + j0 ohm adalah P_T, diberikan oleh 10 log₁₀ (0,125 / P_T) = 1,25. Hasilnya adalah P_T = 0,0937 watt, pengurangan 0,031 watt dari kasus Z_T = Z₀.

Diharapkan untuk membuktikan, menggunakan konsep analisis sirkuit, bahwa untuk semua nilai Zr dan yl reduksi daya yang dikirimkan oleh sumber ke saluran ketika beban terminal menghambat ance diubah dari Z_ (T) = Z_0 ke Zr -r. Zo identik sama dengan jumlah daya gelombang yang diulang kembali ke ujung input garis. Jika P adalah daya input ke garis ketika Zr + Zo, masalahnya adalah untuk menunjukkan itu

Model gelombang pantul yang beraneka ragam hanya berhubungan langsung dengan gelombang arus atau tegangan, bukan dengan daya. Tegangan fasor pada terminal input dari suatu garis adalah jumlah tegangan fasor dari insiden dan gelombang tegangan yang dipantulkan pada titik tersebut, dan fase relatif dari dua tegangan ini dapat memiliki nilai apa pun, tergantung pada koefisien beban beban terminal Pr dan panjang listrik dari garis {Jl dalam radian. untuk rangkaian Gbr. 9-26, ketika input daya ke saluran dikurangi dengan jumlah • ny pantul tenaga gelombang yang mencapai terminal input, ini akan secara umum dihasilkan dari sambungan di kedua daya output dari sinyal sumber, dan jumlah daya yang hilang • i sumber impedansi Zs = Zo.

MASALAH YANG DIPECAHKAN

Masalahnya memiliki dua bagian:

(a) Untuk menunjukkan bahwa pada saluran transmisi yang memiliki redaman yang dapat diabaikan per panjang gelombang ada adalah dua lokasi di setiap setengah panjang gelombang di mana bagian nyata dari masuk yang dinormalisasi adalah kesatuan, untuk menemukan lokasi dari titik-titik ini, dan untuk menentukan susunan yang dinormalisasi pada garis di masing-masing lokasi.

(B) Untuk menemukan panjang garis rintisan lossless dengan sirkuit terbuka atau penghentian sirkuit pendek yang susunan masukannya tidak terdalibrasi akan sama dan berlawanan dengan nilai yang ditemukan dalam (a).

Gbr. 9-27. Penggunaan bagan Smith untuk menyelesaikan prosedur pencocokan rintisan tunggal.

(A) rintisan dapat ditempatkan di + x / λ (WAVELENGTHS TOWARD GENERATOR) atau -x / λ (WAVELENGTHS TOWARD LOAD) dari tegangan minimum dalam pola gelombang berdiri. The kerentanan masukan dinormalisasi dari rintisan ditempatkan di + x / λ harus + b_n,dan kerentanan masukan dinormalisasi dari rintisan ditempatkan di -x / λ harus -bn.

(B) Penentuan panjang rintisan pencocokan.

l₁ adalah untuk stub dengan penghentian sirkuit pendek untuk ditempatkan di + x / λ;

l₂ untuk stub dengan terminasi sirkuit terbuka untuk ditempatkan di + x / λ;

l₃ adalah untuk rintisan dengan singkat sirkuit terminasi untuk ditempatkan di -x / λ;

l₄ adalah untuk stub dengan terminasi sirkuit terbuka untuk ditempatkan di -x / λ.

Erica Dwi Yuni Astuti Nur Ani

Muhammad Fauzan Azmi F