beli domain indonesia, biaya kuliah universitas pancasila, biaya kuliah universitas trisakti, Blok Mesin, cloud hosting indonesia, cloud server indonesia, daftar universitas di indonesia, Danareksa Online Trading, dedicated server indonesia, Desain Mesin, domain dan hosting, domain dan hosting adalah, domain hosting murah, domain murah, domain paling murah, download software pc terbaru, file hosting indonesia, Gambar Mesin, Gambar Mesin Bubut, harga hosting website, harga web hosting, host indonesia, Hosting And Domain, hosting domain, hosting domain murah, Hosting Web, Info Mesin, Jasa Pembuatan Website Iklan Baris, jurusan universitas indonesia, Keamanan Sistem Informasi, Kumpulan Software Komputer, Mesin 4 Tak, Mesin Ayakan Pasir, Mesin Ball Mill, Mesin Blow Moulding, Mesin Briket, Mesin Bubut Universal, Mesin Crusher Batu, Mesin Crusher Plastik, Mesin Genteng, Mesin Giling Cabe, Mesin Giling Ikan, Mesin Giling Kedelai, Mesin Grinder, Mesin Hammer Mill, Mesin Kompos, Mesin Korter, Mesin Mie, Mesin Miling, Mesin Milling Vertikal, Mesin Obras, Mesin Offset Printing, Mesin Pembuat Bakso Ikan, Mesin Pencacah Rumput, Mesin Pendulang Emas, Mesin Penepung, Mesin Pengayak Pasir, Mesin Penggiling Mie, Mesin Penghancur Kayu, Mesin Pengolahan Karet, Mesin Penyedot Pasir, Mesin Perontok Padi, Mesin Pertambangan Emas, Mesin Pertukangan, Mesin Press Hose, Mesin Roll Forming, Mesin Rotary Dryer, Mesin Sedot Pasir, Mesin Serut, Mesin Spray Dryer, Mesin Stone Crusher, Mesin Tahu, Mesin Tepung, Mesin Tusuk Gigi, Mesin Tusuk Sate, Model Baju Bunga, Sistem Basis Data, Sistem Multimedia, Software Untuk Mengakses Internet, Spesifikasi Komputer Server, universitas internasional batam, universitas islam attahiriyah, universitas multimedia nusantara, universitas pendidikan indonesia, usaha kesehatan sekolah, vps indonesia, web hosting gratisan, web hosting indonesia, web hosting support php, Web Hosting Terbaik Di Indonesia, Web Hosting Terbaik Indonesia, web hosting termurah, Webhost Indonesia, webhosting indonesia, webhosting terbaik, website builder indonesia
Maurice Weiner
United Silicon Carbide, Inc.
Dalam beberapa tahun terakhir, cabang kegiatan penelitian baru yang mI. Pendahuluan untuk Jalur Transmisi dan Mereka
Aplikasi untuk Fenomena Elektromagnetik
Maurice Weiner
United Silicon Carbide, Inc.
Dalam beberapa tahun terakhir, cabang kegiatan penelitian baru yang menarik telah muncul, berhubungan
dengan fenomena yang sangat cepat dalam semikonduktor dan gas. Pendahuluan
instrumentasi dan perangkat kecepatan tinggi, dengan skala waktu sering dalam 1 sampai
1000 picosecond, telah mendorong penyelidikan berbagai phe cepat
nomena, termasuk generasi pulsa elektromagnetik dan cahaya, fotokon-
ductivity, longsoran, hamburan, rekombinasi cepat, dan banyak fisik lainnya
proses. Penelitian ini telah didorong oleh beberapa aplikasi [1], [2]. Ini
termasuk pencitraan ultra-pita lebar dan radar, serta ultra-wideband comrnuni-
kation (sehingga menghindari penggunaan kabel atau serat optik). Selain itu, tersedia
kemampuan instrumentasi baru, berkecepatan tinggi telah menyediakan para peneliti dengan
alat yang berharga untuk mempelajari sifat-sifat material yang enarik
telah muncul, berhubungan
dengan fenomena yang sangat cepat dalam semikonduktor dan gas. Pendahuluan
instrumentasi dan perangkat kecepatan tinggi, dengan skala waktu sering
dalam 1 sampai
1000 picosecond, telah mendorong penyelidikan berbagai phe cepat
nomena, termasuk generasi pulsa elektromagnetik dan cahaya, fotokon-
ductivity, longsoran, hamburan, rekombinasi cepat, dan banyak fisik lainnya
proses. Penelitian ini telah didorong oleh beberapa aplikasi [1], [2]. Ini
termasuk pencitraan ultra-pita lebar dan radar, serta ultra-wideband
comrnuni-
kation (sehingga menghindari penggunaan kabel atau serat optik). Selain
itu, tersedia
kemampuan instrumentasi baru, berkecepatan tinggi telah menyediakan para
peneliti dengan
alat yang berharga untuk mempelajari sifat-sifat material yang mendasar. Di
semua
aplikasi tersebut, fitur utama adalah generasi electromag-
pulsa netic dengan durasi pulsa yang sempit atau penelitianime cepat (atau
keduanya). Itu
interval waktu singkat yang terlibat (baik dalam durasi penelitianime atau
pulsa), menjamin
bahwa spektrum frekuensi yang luas dihasilkan, sebuah properti yang sangat
penting untuk
aplikasi yang dikutip.
Pemahaman fenomena cepat dan ultra-wideband elektromagnetik
sumber dibuat lebih rumit oleh waktu penelitian yang sangat cepat dan
berdasarkan fakta
bahwa panjang gelombang dari sinyal yang dihasilkan seringkali lebih kecil
atau
sebanding dengan panjang
karakteristik perangkat atau eksperimental
konfigurasi yang sedang diteliti. Akibatnya penggunaan variabel sirkuit disamakan adalah
tidak pantas dan kita harus menggunakan variabel saluran transmisi atau Maxwell
persamaan langsung.
/
2 Analisis Elektromagnetik Menggunakan Variabel Saluran Transmisi
Sinyal elektromagnetik dengan panjang gelombang sangat pendek dapat dihasilkan oleh a
transisi mendadak dalam konduktivitas medium. Anggaplah, misalnya, sebuah
bias medan listrik pertama diterapkan pada medium dan yang selanjutnya
konduktivitas sebagian media tiba-tiba meningkat (misalnya, oleh
fotokonduktivitas atau longsoran salju). Perubahan mendadak dalam konduktivitas akan
menghasilkan pulsa elektromagnetik dengan risetimes sangat curam, sehingga menghasilkan pendek
sinyal panjang gelombang. Dalam kasus di mana cahaya dihasilkan (misalnya, saat operator
bergabung kembali dalam galium arsenide), panjang gelombang secara alami akan lebih kecil atau di
paling tidak sebanding dengan ukuran perangkat. Bagaimanapun, analisis sering digunakan untuk
mendeskripsikan perangkat dan konfigurasi eksperimental tidak cukup menjawab
sinyal panjang gelombang pendek yang dihasilkan, dan kemudian tersebar
di seluruh perangkat dan ruang sekitarnya. Seseorang seharusnya tidak meremehkan
pentingnya penyebaran energi elektromagnetik (yang meliputi cahaya
sinyal). Seringkali fisika dari proses yang mendasari disalahpahami karena
penyebaran energi elektromagnetik, yang mengantarkan fisika ke detektor,
tidak diperhitungkan dengan baik, terutama untuk fenomena cepat. Diharapkan
diskusi berikutnya akan membantu memperbaiki kekurangan ini dan mengarah ke yang lebih baik
pemahaman tentang penyebaran sinyal elektromagnetik ultra-wideband dan
fenomena terkait.
Dalam buku ini kami berusaha untuk menggambarkan fenomena elektromagnetik yang cepat,
bergantung pada persamaan tingkat iteratif yang menggunakan matriks saluran transmisi (TLM)
variabel. Seperti halnya teknik numerik yang sebanding, seperti yang terbatas
metode perbedaan, elemen saluran transmisi harus dibuat sangat kecil di
untuk mencapai ketepatan, dan solusi pada langkah waktu tertentu bergantung pada a
pengetahuan tentang solusi pada langkah waktu sebelumnya. Dari segi fisik
interpretasi dan intuisi, bagaimanapun, metode TLM jauh lebih unggul daripada itu
perbedaan terbatas atau teknik numerik serupa lainnya. Daya tarik fisik
metode TLM dapat dilihat, dengan cara konseptual, dari dua dasar
komponen yang terdiri dari matriks TLM: saluran transmisi dan
node yang membentuk perpotongan garis, seperti yang tercantum pada Gambar. 1.1. Dengan ini
model, kita secara konseptual dapat memisahkan fisika dan penyebaran energi yang diberikan
masalah dalam elektromagnetik. Dengan demikian, node mewakili fisika, dan
proses fisik (seperti perubahan konduktivitas) dipetakan ke node,
yang kemudian mengontrol aliran energi di jalurnya. Komponen lainnya, the
saluran transmisi, bertanggung jawab untuk distribusi energi dan penyimpanan
konfigurasi yang sedang diteliti. Akibatnya penggunaan variabel sirkuit disamakan adalah
tidak pantas dan kita harus menggunakan variabel saluran transmisi atau Maxwell
persamaan langsung.
/
2 Analisis Elektromagnetik Menggunakan Variabel Saluran Transmisi
Sinyal elektromagnetik dengan panjang gelombang sangat pendek dapat dihasilkan oleh a
transisi mendadak dalam konduktivitas medium. Anggaplah, misalnya, sebuah
bias medan listrik pertama diterapkan pada medium dan yang selanjutnya
konduktivitas sebagian media tiba-tiba meningkat (misalnya, oleh
fotokonduktivitas atau longsoran salju). Perubahan mendadak dalam konduktivitas akan
menghasilkan pulsa elektromagnetik dengan risetimes sangat curam, sehingga menghasilkan pendek
sinyal panjang gelombang. Dalam kasus di mana cahaya dihasilkan (misalnya, saat operator
bergabung kembali dalam galium arsenide), panjang gelombang secara alami akan lebih kecil atau di
paling tidak sebanding dengan ukuran perangkat. Bagaimanapun, analisis sering digunakan untuk
mendeskripsikan perangkat dan konfigurasi eksperimental tidak cukup menjawab
sinyal panjang gelombang pendek yang dihasilkan, dan kemudian tersebar
di seluruh perangkat dan ruang sekitarnya. Seseorang seharusnya tidak meremehkan
pentingnya penyebaran energi elektromagnetik (yang meliputi cahaya
sinyal). Seringkali fisika dari proses yang mendasari disalahpahami karena
penyebaran energi elektromagnetik, yang mengantarkan fisika ke detektor,
tidak diperhitungkan dengan baik, terutama untuk fenomena cepat. Diharapkan
diskusi berikutnya akan membantu memperbaiki kekurangan ini dan mengarah ke yang lebih baik
pemahaman tentang penyebaran sinyal elektromagnetik ultra-wideband dan
fenomena terkait.
Dalam buku ini kami berusaha untuk menggambarkan fenomena elektromagnetik yang cepat,
bergantung pada persamaan tingkat iteratif yang menggunakan matriks saluran transmisi (TLM)
variabel. Seperti halnya teknik numerik yang sebanding, seperti yang terbatas
metode perbedaan, elemen saluran transmisi harus dibuat sangat kecil di
untuk mencapai ketepatan, dan solusi pada langkah waktu tertentu bergantung pada a
pengetahuan tentang solusi pada langkah waktu sebelumnya. Dari segi fisik
interpretasi dan intuisi, bagaimanapun, metode TLM jauh lebih unggul daripada itu
perbedaan terbatas atau teknik numerik serupa lainnya. Daya tarik fisik
metode TLM dapat dilihat, dengan cara konseptual, dari dua dasar
komponen yang terdiri dari matriks TLM: saluran transmisi dan
node yang membentuk perpotongan garis, seperti yang tercantum pada Gambar. 1.1. Dengan ini
model, kita secara konseptual dapat memisahkan fisika dan penyebaran energi yang diberikan
masalah dalam elektromagnetik. Dengan demikian, node mewakili fisika, dan
proses fisik (seperti perubahan konduktivitas) dipetakan ke node,
yang kemudian mengontrol aliran energi di jalurnya. Komponen lainnya, the
saluran transmisi, bertanggung jawab untuk distribusi energi dan penyimpanan
Baris TLM dapat dianggap
memiliki tingkat spasial, sedangkan node berada
dianggap sebagai sangat kecil.
Dalam komunitas teknik elektro, penggunaan saluran transmisi
variabel untuk mengobati satu masalah elektromagnetik dimensi telah diperoleh
popularitas selama bertahun-tahun. Akibatnya, tingkat kenyamanan tertentu telah tercapai
oleh insinyur dalam penggunaan terminologi saluran transmisi. Akumulasi dari
Deskripsi TLM untuk masalah elektromagnetik dua dan tiga dimensi,
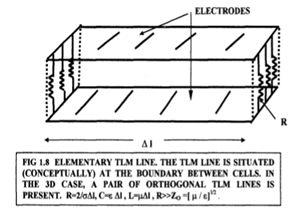
Gambar tersebut menunjukkan pandangan sisi dua elektroda dipisahkan oleh semi-
bahan konduktor, dengan bias medan listrik antara dua elektroda. Sup-
pose wilayah terbatas semikonduktor, ditunjukkan oleh wilayah yang gelap, adalah
tiba-tiba dibuat (baik dengan pulsa cahaya atau oleh longsoran yang terlokalisasi dan cepat
kerusakan). Ini akan menimbulkan gangguan elektromagnetik dan mungkin a
pulsa cahaya (tergantung pada medium), yang berasal dari wilayah konduksi.
Kurva putus-putus mungkin secara konseptual dianggap sebagai kontur amplitudo yang sama
dari gangguan elektromagnetik pada suatu saat tertentu. Sebagaimana dicatat para
turbance diasumsikan asimetris, karena amplitudonya akan lebih pro-
diucapkan ke arah tegak lurus terhadap bidang bias. Seseorang dapat menganggap
gangguan elektromagnetik sebagai gelombang perjalanan yang dibuat oleh bagian awal
lapangan yang sejajar dengan permukaan daerah konduksi diaktifkan. Itu
gelombang, yaitu gangguan, direfleksikan secara normal dari permukaan aktivasi
wilayah tion saat menjalani inversi medan listrik, sehingga total bidang, di
dianggap sebagai sangat kecil.
Dalam komunitas teknik elektro, penggunaan saluran transmisi
variabel untuk mengobati satu masalah elektromagnetik dimensi telah diperoleh
popularitas selama bertahun-tahun. Akibatnya, tingkat kenyamanan tertentu telah tercapai
oleh insinyur dalam penggunaan terminologi saluran transmisi. Akumulasi dari
Deskripsi TLM untuk masalah elektromagnetik dua dan tiga dimensi,
Gambar tersebut menunjukkan pandangan sisi dua elektroda dipisahkan oleh semi-
bahan konduktor, dengan bias medan listrik antara dua elektroda. Sup-
pose wilayah terbatas semikonduktor, ditunjukkan oleh wilayah yang gelap, adalah
tiba-tiba dibuat (baik dengan pulsa cahaya atau oleh longsoran yang terlokalisasi dan cepat
kerusakan). Ini akan menimbulkan gangguan elektromagnetik dan mungkin a
pulsa cahaya (tergantung pada medium), yang berasal dari wilayah konduksi.
Kurva putus-putus mungkin secara konseptual dianggap sebagai kontur amplitudo yang sama
dari gangguan elektromagnetik pada suatu saat tertentu. Sebagaimana dicatat para
turbance diasumsikan asimetris, karena amplitudonya akan lebih pro-
diucapkan ke arah tegak lurus terhadap bidang bias. Seseorang dapat menganggap
gangguan elektromagnetik sebagai gelombang perjalanan yang dibuat oleh bagian awal
lapangan yang sejajar dengan permukaan daerah konduksi diaktifkan. Itu
gelombang, yaitu gangguan, direfleksikan secara normal dari permukaan aktivasi
wilayah tion saat menjalani inversi medan listrik, sehingga total bidang, di
Introduction to Transmission Lines 5

sekitar langsung dari wilayah
konduksi awal, sebagian atau seluruhnya
dibatalkan (tergantung pada tingkat konduktivitas). Situasi berubah, dari
Tentu saja, jika gangguan gelombang awal mengalami pembalikan medan tambahan di
batas konduktor terdekat, yang dapat menjadi salah satu dari dua elektroda atau
beberapa konduktor tambahan (seperti anggota saluran transmisi yang di-ground).
Perubahan dalam gangguan gelombang juga dapat terjadi, tentu saja, karena adanya
tence dari antarmuka dielektrik.
Hasil akhirnya adalah susunan gelombang yang kompleks di seluruh wilayah, di mana
konfigurasi lapangan tergantung pada sifat temporal dan spasial dari
wilayah konduksi, serta geometri perangkat. Dengan kondisi seperti itu, maka
bidang akan berubah secara dramatis (dibandingkan dengan seragam awal, bidang statis) dan
daerah pengurangan bidang atau peningkatan lapangan kemungkinan akan terjadi.
Jika cahaya diproduksi di semikonduktor, situasinya ada di beberapa
cara-cara yang lebih mudah untuk dijelaskan, dan dengan cara lain itu lebih rumit. Cahaya
profil gangguan akan lebih simetris, dibandingkan dengan
depan elektromagnetik, karena panjang gelombang yang lebih pendek dan sifat acak
bahkan tanpa pembenihan operator langsung, longsoran salju dapat diproduksi di suatu wilayah
yang jauh dari situs asli dari cahaya pelampiasan, yang disebabkan oleh
augmentasi medan elektromagnetik (mengikuti kesal awal
medan statis) di berbagai daerah. Metode TLM sangat cocok untuk memperoleh
seperti ekstensi konduktivitas
1.2 Contoh Sumber Impuls
diingat bahwa sumber lain dari konduktivitas (seperti longsoran atau
injeksi pembawa) dapat dimasukkan ke dalam formulasi TLM.
Sebagai contoh pertama, Gambar. 1.3, pertimbangkan jalur transmisi pelat sejajar di
yang sebagian dari konduktor atas telah dihapus dan diganti dengan
dibatalkan (tergantung pada tingkat konduktivitas). Situasi berubah, dari
Tentu saja, jika gangguan gelombang awal mengalami pembalikan medan tambahan di
batas konduktor terdekat, yang dapat menjadi salah satu dari dua elektroda atau
beberapa konduktor tambahan (seperti anggota saluran transmisi yang di-ground).
Perubahan dalam gangguan gelombang juga dapat terjadi, tentu saja, karena adanya
tence dari antarmuka dielektrik.
Hasil akhirnya adalah susunan gelombang yang kompleks di seluruh wilayah, di mana
konfigurasi lapangan tergantung pada sifat temporal dan spasial dari
wilayah konduksi, serta geometri perangkat. Dengan kondisi seperti itu, maka
bidang akan berubah secara dramatis (dibandingkan dengan seragam awal, bidang statis) dan
daerah pengurangan bidang atau peningkatan lapangan kemungkinan akan terjadi.
Jika cahaya diproduksi di semikonduktor, situasinya ada di beberapa
cara-cara yang lebih mudah untuk dijelaskan, dan dengan cara lain itu lebih rumit. Cahaya
profil gangguan akan lebih simetris, dibandingkan dengan
depan elektromagnetik, karena panjang gelombang yang lebih pendek dan sifat acak
bahkan tanpa pembenihan operator langsung, longsoran salju dapat diproduksi di suatu wilayah
yang jauh dari situs asli dari cahaya pelampiasan, yang disebabkan oleh
augmentasi medan elektromagnetik (mengikuti kesal awal
medan statis) di berbagai daerah. Metode TLM sangat cocok untuk memperoleh
seperti ekstensi konduktivitas
1.2 Contoh Sumber Impuls
diingat bahwa sumber lain dari konduktivitas (seperti longsoran atau
injeksi pembawa) dapat dimasukkan ke dalam formulasi TLM.
Sebagai contoh pertama, Gambar. 1.3, pertimbangkan jalur transmisi pelat sejajar di
yang sebagian dari konduktor atas telah dihapus dan diganti dengan
Introduction to Transmission Lines 7
semikonduktor, mampu menahan
tegangan. Garis tersebut kemudian dibebankan hingga
tegangan, menghasilkan medan, sebagaimana ditunjukkan dalam semikonduktor, serta a
medan fringing antara dua konduktor. Penciptaan operator yang tiba-tiba dengan
pulsa ringan, di seluruh semikonduktor, atau bahkan dalam porsi terbatas
semikonduktor, kemudian menghasilkan pulsa risetime cepat yang bergerak ke bawah
garis ke arah output, biasanya sebuah antena.
8 Analisis Elektromagnetik Menggunakan Variabel Saluran Transmisi
ditunjukkan pada Gambar. 1.4. Energi elektrostatik awal disimpan dengan tegangan bias
antara konduktor saluran transmisi strip. Konduktor menyimpang sebagai
ditunjukkan untuk membentuk trafo / antena komposit. Saklar, dalam bentuk sebuah
semikonduktor aktif optik, terletak di ujung impedansi rendah
transformator. Ketika semikonduktor tiba-tiba diaktifkan, pulsa terbalik
diluncurkan ke arah output antena. Metode TLM kemudian dapat digunakan
untuk menentukan bidang di seluruh ruang, yaitu semikonduktor, trans
daerah bekas dan radiasi. Gambar 1.5 menunjukkan versi lain dari suatu impuls
sumber yang terdiri dari dua elektroda konduktif yang ditempatkan pada dielektrik
substrat.
tegangan, menghasilkan medan, sebagaimana ditunjukkan dalam semikonduktor, serta a
medan fringing antara dua konduktor. Penciptaan operator yang tiba-tiba dengan
pulsa ringan, di seluruh semikonduktor, atau bahkan dalam porsi terbatas
semikonduktor, kemudian menghasilkan pulsa risetime cepat yang bergerak ke bawah
garis ke arah output, biasanya sebuah antena.
8 Analisis Elektromagnetik Menggunakan Variabel Saluran Transmisi
ditunjukkan pada Gambar. 1.4. Energi elektrostatik awal disimpan dengan tegangan bias
antara konduktor saluran transmisi strip. Konduktor menyimpang sebagai
ditunjukkan untuk membentuk trafo / antena komposit. Saklar, dalam bentuk sebuah
semikonduktor aktif optik, terletak di ujung impedansi rendah
transformator. Ketika semikonduktor tiba-tiba diaktifkan, pulsa terbalik
diluncurkan ke arah output antena. Metode TLM kemudian dapat digunakan
untuk menentukan bidang di seluruh ruang, yaitu semikonduktor, trans
daerah bekas dan radiasi. Gambar 1.5 menunjukkan versi lain dari suatu impuls
sumber yang terdiri dari dua elektroda konduktif yang ditempatkan pada dielektrik
substrat.


Seseorang dapat menduga bahwa
mendapatkan praktis, kuantitatif, dan akurat
solusi elektromagnetik untuk konfigurasi di atas akan nampak seperti a
tugas yang tangguh, terutama jika kita harus bergantung pada analisis numerik, berdasarkan
pada persamaan Maxwell, kondisi batas, serta fisika
mendasari berbagai fenomena seperti phtoconductivity, longsoran salju,
rekombinasi, dll ...
solusi elektromagnetik untuk konfigurasi di atas akan nampak seperti a
tugas yang tangguh, terutama jika kita harus bergantung pada analisis numerik, berdasarkan
pada persamaan Maxwell, kondisi batas, serta fisika
mendasari berbagai fenomena seperti phtoconductivity, longsoran salju,
rekombinasi, dll ...
dipetakan ke simpul, yaitu persimpangan dari
saluran transmisi. Metode ini, oleh karena itu, membuat pemisahan antara
penyebaran energi dan fisika. Garis besar model saluran transmisi, dan
hubungannya dengan teknik nwnerical standar, menggunakan perbedaan yang
terbatas, dijelaskan dalam bagian berikut.
1.3 Model Garis Besar
Pengembangan model saluran transmisi dimulai dengan persamaan gelombang Maxwell [3], termasuk istilah konduktivitas (unit MKS digunakan). Demikian,
dimana: v 2E - (l / v2) (& Elfi2) - µa (oE / at) = o
E = Medan Listrik
(I.I)
t = waktu
µ = permeabilitas
v = kecepatan propagasi
a = konduktivitas
Persamaan (1.1) tidak ada muatan yang benar dalam medium. Persamaan serupa juga berlaku untuk medan magnet. Seperti disebutkan sebelumnya, metode numerik dapat digunakan untuk mendapatkan solusi untuk Persamaan (1.1). Daripada mengikuti jalan ini. Namun, pendekatan saluran transmisi diselidiki. Namun, tujuan saya adalah, pertama-tama kita harus mempertimbangkan kasus satu dimensi. Dengan demikian, persamaan gelombang kemudian bC) muncul
& Ela,? - - (1tv2) (& E1or) - µa (aE1at) = o (1.2)
konvergensi merikal, waktu propagasi sel, Aliv, harus jauh lebih kecil dari waktu relaksasi, Ela. Al karenanya harus memuaskan Al << ev / a. Selain itu, Al harus jauh lebih kecil daripada panjang cb.aracteristic yang terkait dengan, misalnya, geometri atau kondisi eksperimental lainnya. Jelas, semakin kecil ukuran ukuran sel, semakin besar resolusinya, meskipun ini menempatkan beban yang lebih besar pada kecepatan dan memoi komputer.Persamaan (1.2) identik dengan persamaan saluran transmisi yang dikenal, yang mengatur tegangan V untuk saluran transmisi satu dimensi menggunakan variabel rangkaian, seperti ditunjukkan Gambar.1.6, av210x '- (L'C'Xfi-VJor) -L'O' (oV / iJt): 0 (1.3)
Analisis Elektromagnetik Menggunakan Variabel Saluran TransmisiTabel 1.1 menunjukkan hubungan antara persamaan gelombang menggunakan variabel lapangan, Persamaan (1.2), dan bahwa menggunakan variabel rangkaian, Persamaan (1.3). Penyederhanaan penting terjadi ketika kita memilih elemen saluran transmisi kecil (atau sel) dari panjang Al. Adalah berguna untuk menyatakan total kapasitansi, induktansi, dan konduktansi yang terkait dengan elemen garis, yang kita identifikasikan sebagaiC = C'Al = sAl (1.4a)L = L'Al = nAl (1.4b)G = GÁl = aA1 (1.4c)Resistansi total R dari unsur demikian R = l / G. Waktu relaksasi, e / o \ sama dengan waktu "RC" untuk sel, sebagaimana dicatat dari Persamaan (1.4). Kami juga mengidentifikasi impedansi dari garis sebagaiPada titik ini kita dapat mengukur pemilihan Al. Untuk mendapatkan akurasi, kami memilih Al seperti ituPersamaan (1.6) - (1.7) menyatakan bahwa penundaan waktu transit dalam sel Al, sama dengan Al / v, jauh lebih kecil daripada waktu RC sel. Sebuah pernyataan ekuivalen adalah bahwa resistensi terpusat, R, dari elemen Al jauh lebih besar daripada impedansi karakteristik, Z0, atauBerdasarkan persamaan sebelumnya, L ', C dapat digabungkan menjadi elemen transmisi lossless, Z0, dan konduktansi dapat digabungkan menjadi dua resistor, R, yang terletak di ujung saluran transmisi, seperti ditunjukkan pada Gambar 1.7, di mana R diberikan olehDua faktor muncul dalam Persamaan (1.9) karena masing-masing dari dua resistor, R, dapat dianggap secara paralel. Cara lain untuk melihat pengenalan dua faktor adalah sebagai berikut. Dengan memfokuskan elemen baris TLM tunggal, kami mengabaikan elemen TLM yang bersebelahan, masing-masing dengan resistor ujung yang serupa; karena resistor yang bersebelahan secara paralel, dua faktor harus diperkenalkan ketika "mengekstraksi" satu elemen dari rantai.
Dalam arti kami menganggap garis TLM sebagai dikelilingi oleh permeabilitas tinggi, media impedansi tinggi. Satu-satunya fungsi dari garis TLM adalah untuk mensimulasikan bidang dalam medium. Dalam hal apapun, bahkan tanpa asumsi ini, bidang-bidang pinggiran di garis TLM tetangga akansehingga sel yang berdekatan memiliki resistivitas yang tidak sama(tetapi konstanta dielektrik yang sama).Untuk baris ini, konduktansi di setiap node akan ditambahkan dan dengan demikianresistor yang sesuai akan ditambahkan secara paralel, sehingga
Pengantar Jalur Transmisi 19
Demikian pula ada dua jalur transmisi jalur transmisi yang terkait
setiap ujung kubus, yang membuat analisis lebih rumit. A disederhanakan
deskripsi matriks 2D diberikan nanti dalam Bab ini. Rinci
deskripsi dari kedua matriks 2D dan 3D, dalam notasi seluler , diberikan dalam
Bab II-IV.
1.4 Aplikasi Model untuk Resistensi Node Kecil
Kami telah mengadopsi model di mana resistansi sel node jauh lebih besar daripada
impedansi saluran sel. Dengan kata lain, kami memberlakukan syarat bahwa
waktu transit sel Di jauh lebih kecil dari waktu RC konstan.
Kapanpun konduktivitas yang kuat dimasukkan ke dalam medium, model
meminta kita untuk memeriksa ukuran matriks sel, dan untuk menggunakan ukuran kecil yang sesuai
sel. Ukuran sel yang kecil secara alami mengimplikasikan ukuran larik yang lebih besar, dengan berikutnya
kompleksitas dalam simulasi komputer. Apa implikasi dari mempertahankan
sel yang lebih besar, yang tidak memuaskan R »Z 0 ? Tentu saja, penggunaan sel-sel yang lebih besar
menyederhanakan proses komputer.
20 Analisis Elektromagnetik Menggunakan Variabel Saluran Transmisi
Wilayah R «Z0 ada, dan juga di App.7A.4 di mana kita membahas lapangan
disipasi dalam hal gelombang TLM dasar.
1.5 Latar Belakang Teori Saluran Transmisi
Diskusi di bagian sebelumnya akan dikuantifikasi dan didamaikan
teori saluran transmisi. seperti yang ditunjukkan pada
Gambar 1.12 (a) Analisis dilanjutkan dengan terlebih dahulu memilih set normal yang benar
mode yang mendeskripsikan gelombang berdiri selama off-state, ketika garis tersebut
bias ke tegangan V0. Ini tidak sulit didapat, karena kita tahu itu jenderal
solusi untuk persamaan gelombang (Persamaan (1.2)), atau Persamaan yang setara (1.3). Membuang
istilah konduktivitas, solusinya adalah sepasang gelombang yang bergerak berlawanan
arah dengan kecepatan, v. Kumpulan mode paling sederhana yang memenuhi
kondisi batas, selama off-state, adalah dua gelombang masing-masing dengan amplitudo konstan,
masing-masing sama dengan setengah tegangan bias, Vo / 2. Kedua gelombang bergerak berlawanan
arah, dan ditunjuk + V dan ~ V pada Gambar. 1.12. + V menandakan
gelombang bepergian dalam arah x plus sementara ~ V adalah gelombang perjalanan yang mundur
dalam arah x negatif.
Gelombang tegangan mengisi seluruh elemen transmisi dan dibatasi
oleh sirkuit terbuka di kedua ujungnya, di mana gelombang dipantulkan sehingga + V mengkonversi
ke "V di satu ujung, dan sebaliknya di ujung yang lain. Gelombang mematuhi
persyaratan simetri dan tentu saja gelombang menindih untuk memberikan yang benar
tegangan setiap saat dan pada semua titik di garis selama kesetimbangan, yaitu, V0 = + V
+ - y = + (Vo / 2) + "(Vo / 2). Dengan demikian, solusi umum untuk tegangan terdiri
Pengantar Jalur Transmisi 21
22 Analisis Elektromagnetik Menggunakan Variabel Saluran Transmisi
Dengan cara yang sama, amplitudo maju dan mundur saat ini dinotasikan oleh + I dan ~ I, masing-masing, dan arus total adalah
I = + I + ~ I (1.11)
Selanjutnya kita tuliskan hubungan antara tegangan dan arus
ombak:
+ I = + V / Z 0 (1,12)
~ I = - ~ V / Z 0 (1.13)
di mana Z G adalah impedansi karakteristik dari garis. Tanda minus untuk
arus balik gelombang signifikan. Meskipun gelombang tegangan mundur mungkin
menjadi positif, arus gelombang mundur akan negatif, dan merupakan indikasi dari
Fakta bahwa arus bergerak ke arah negatif, jauh dari beban.
Selanjutnya, kami mencatat kondisi batas yang ada pada beban. Jika RL adalah
beban (diasumsikan nyata) di persimpangan, kemudian pada beban V dan saya puas
V = R L I (1.14)
Pada titik ini kita mendefinisikan dua jenis koefisien tegangan. Koefisien refleksi,
B, menghubungkan gelombang yang dipantulkan ~ V ke gelombang datang + V, sedangkan
koefisien transfer, T, menghubungkan tegangan beban V dengan gelombang datang. Demikian,
B = 'V / + V (1.15)
T = R L I / + V (1.16)
Jika Persamaan (1,10) - (1,14) digunakan maka koefisien ini menjadi
B = (RL-Z 0 ) / (RL + Z 0 ) (1,17)
dan
Pengantar Jalur Transmisi 23
T = 2R L / (R L + Z 0 ) (1,18)
Koefisien ini memainkan peran penting dalam penyebaran elektromagnetik
sinyal karena konduktivitas. Seseorang harus menunjukkan bahwa RL mungkin termasuk tidak hanya
resistor pengakhir, tetapi juga impedansi karakteristik dari setiap yang bersebelahan
saluran transmisi. Jika sel sebelah memiliki impedansi, Z u dan persimpangan
resistansi adalah R, maka impedansi beban dilihat oleh gelombang di Z D , adalah paralel
kombinasi yang diberikan oleh R L = ZyRJ [R + Zi]. Perhatikan bahwa ketika Zi = Z 0 dan R ~ oo
sel impedansi dicocokkan, T = 1, B = 0, dan gelombang mengalir ke sel yang bersebelahan
leluasa.
Adalah wajar untuk menanyakan apakah koefisien transfer dan refleksi itu
terkait, berdasarkan pertimbangan aliran energi. Dugaan ini memang benar
dikonfirmasi dengan mempertimbangkan hubungan berikut:
(T 2 / R L ) + (B 2 / Z 0 ) = 1 / Z 0 (1,19)
Substitution of Eqs. (1.17) - (1.18) menjadi Persamaan (1.19) memverifikasi hubungan.
Persamaan (1.19) memiliki interpretasi yang sangat sederhana. Jika gelombang dengan amplitudo unit, menyebar
sejalan Z 0, bertemu node dengan impedansi beban RL, maka Persamaan. (1.19)
hanya menyatakan bahwa aliran energi insiden, 1 / Z 0 , sama dengan aliran energi yang dikirimkan
ke R L (yaitu, T 2 / R L ) ditambah aliran energi yang dipantulkan dari beban (yaitu,
B 2 / Z Q ). Mengetahui salah satu koefisien, bagaimanapun, tidak secara otomatis menyediakan
kita dengan yang lain. Misalnya, menghitung B dari Persamaan (1.19) (berdasarkan pada
pengetahuan tentang T) meninggalkan kita dengan ambiguitas seperti tanda B; asli
definisi B, Persamaan (1.17), harus digunakan. Dari Persamaan (1.17) kita melihat, oleh karena itu,
bahwa B positif ketika RL melebihi Zo dan negatif ketika R L kurang dari Z 0 .
Di paragraf sebelumnya kami menggambarkan situasi di mana gelombang tunggal
di saluran transmisi terjadi insiden pada impedansi beban. Sekarang anggap saja
beban tidak lebih dari saluran transmisi lain dengan impedansi yang berbeda,
dan selanjutnya misalkan baris kedua juga memiliki insiden sinyal pada node
memisahkan dua jalur transmisi. Situasi diilustrasikan pada Gambar. 1.13
di mana dua garis TLM adalah Z A dan Z B dan gelombang insiden yang terkait
voltase adalah + VA dan ~ VB- Ketika kita menerapkan teori TLM pada situasi ini, tidak
interpretasi kami terhadap hasil berubah secara signifikan? Kami melanjutkan
24 Analisis Elektromagnetik Menggunakan Variabel Saluran Transmisi
dengan menerapkan formulasi TLM secara individual untuk masing-masing dari dua insiden tersebut
gelombang + VA dan "V B. Dalam kasus + V A , RL = ZB, dan ini menghasilkan a
gelombang yang ditransmisikan [2ZB / (ZA + Z B )] * + V A dan gelombang yang dipantulkan [(Z B Z A ) /
ZA + Z B)] * + V A. Demikian juga, dalam kasus ~ V B , beban yang dilihat oleh "V B adalah ZA,
dan gelombang yang ditransmisikan dan dipantulkan adalah [2Z A / (Z A + Z B )] * ~ V B dan [(Z A Z B ) /
ZA + Z B )] * ~ VB masing-masing. Menambahkan hasil (linear) di setiap baris untuk
kedua gelombang dapat memeriksa bahwa kontinuitas tegangan pada node adalah
diawetkan di hadapan dua gelombang insiden. Kami pertama kali mendapatkan dua gelombang
bergerak menjauh dari node. Total gelombang mundur dalam Z A akan
"V A = [(Z B -Z A ) / Z A + Z B )] * + V A + [2Z A / (Z A + Z B )] *" V B (1,20)
sedangkan gelombang maju dalam Z B akan
+ V B = [(Z A -Z B ) / Z A + ZB)] * "V B + [2ZB / (Z A + Z B )] * + V A (1,21)
Kami kemudian dapat memverifikasi bahwa tegangan total pada node adalah V = + V A + ~ V A = + V B + ~ VB It
berguna untuk memastikan bahwa energi gelombang terbawa dari
Pengantar Jalur Transmisi 25
node, terkait dengan V A dan + VB, menjaga aliran energi. Kami tahu itu
Insiden aliran energi total pada node, E T , diberikan oleh
E T = (1 / ZA) ( + V A ) 2 + (1 / Z B ) CV B ) 2 (1,22)
Maka mudah untuk memverifikasi bahwa energi yang terbawa dari node memenuhi
E T = (1 / ZA) ( + V A ) 2 + (1 / Z B ) CV B ) 2 = (1 / Z A ) fV A ) 2 + (1 / Z B ) ( + V B ) 2 ( 1-23)
menggunakan Persamaan (1.20) dan (1.21). Kita harus berhati-hati untuk memperhatikan perubahan gelombang
arah dalam Persamaan (1,22) dan (1,23). Kami belum memasukkan kerugian, yang diwakili oleh
R di simpul. Jika kita melakukannya, maka selain energi gelombang terbawa
oleh "V A dan + V B, akan ada kerugian resistif diberikan oleh V 2 / R, tetapi hanya seperti sebelumnya
V = + V A + V A = + V B + -V B.
1.6 Ketentuan Awal Minat Khusus
Sebelum kita menerapkan konsep saluran transmisi dan hubungan ke iteratif
metode, pertama-tama kita periksa konsistensi model dalam kondisi awal
minat khusus. Pertama kita mempertimbangkan apakah rantai saluran transmisi ID, sebagai
ditunjukkan pada Gambar. 1,14, stabil, yaitu, tetap dalam kesetimbangan bahkan ketika resistor node,
R, tidak diaktifkan dan garis sel masing-masing bias ke tegangan yang sama .
Untuk mencapai tujuan ini, kami menganggap resistor akhir jauh lebih besar daripada karakteristiknya
impedansi garis. Seperti yang tercantum pada Gambar 1.14 tiga garis yang bersebelahan
memiliki impedansi karakteristik yang sama. Untuk t> 0, total impedansi beban terlihat
oleh gelombang maju dalam A akan menjadi RL = Z 0 , karena kombinasi paralel R dan
Z „hanya Z 0 , karena R sangat besar. Jadi gelombang maju dari garis A
ke baris B akan terhalang (yaitu, "cocok" ke B). Begitu pula dengan gelombang kebelakang
dalam B akan dicocokkan dengan A. Komentar serupa berlaku untuk garis B dan C. Efek bersih
adalah bahwa kondisi kesetimbangan di jalur B (atau sel lain dalam rantai)
tetap sama, dengan gelombang maju dan mundur yang sama (dan dengan sama
amplitudo) seperti pada langkah waktu sebelumnya. Kesetimbangan juga dipertahankan ketika
impedansi sel yang berdampingan tidak sama. Dengan demikian tidak ada transfer bersih
26 Analisis Elektromagnetik Menggunakan Variabel Saluran Transmisi
energi dari satu sel ke sel lainnya.
Ini juga menarik untuk menentukan peluruhan berbagai sel untuk seragam
Rantai ID di mana setiap sel awalnya bias ke V 0 dan resistansi simpul R adalah
terbatas dan seragam di seluruh rantai. Dalam situasi seperti ini orang bisa menggunakannya
Persamaan (1.17) - (1.18) untuk menentukan peluruhan dalam setiap sel. Untuk R besar (relatif
ke garis impedansi) gelombang maju dan mundur membusuk dengan jumlah (1-
Z „/ R) dengan setiap langkah waktu. Karena hambatan simpul dan impedansi garis
Seragam, bagaimanapun, kita dapat mengadopsi pandangan bahwa tidak ada transfer energi bersih
dari satu sel ke sel lainnya.
Pengantar Jalur Transmisi 27
sendiri di antara sel dan transfer energi bersih dari satu sel ke sel lainnya
akan terjadi. Apa yang terjadi ketika garis-garis yang bersebelahan awalnya bias menjadi berbeda
tegangan, bahkan ketika resistor node tak terhingga besar dan sel
impedansi seragam? Gelombang maju dari A ke B tidak akan
dikompensasi oleh gelombang ke belakang dari B ke A. Ekuilibrium karenanya
tidak dikelola untuk array satu dimensi.
Analisis TLM Satu Dimensi. Perbandingan dengan Selisih Terbatas
metode
I. 7 Metode Iterasi TLM
Kami memulai perbandingan ID TLM dan metode beda hingga dengan terlebih dahulu
mempertimbangkan iterasi TLM. Untuk kesederhanaan kita mengasumsikan resistensi yang sama,
R, memisahkan garis yang bersebelahan, yang memiliki impedansi karakteristik yang sama
Z 0 . Selama interval waktu tertentu, jumlah gelombang maju dan mundur,
+ V dan "V, terdiri dari total bidang V. Seperti yang disebutkan sebelumnya, gelombang lapangan mungkin
ditulis dalam hal bidang milik interval sebelumnya. Menggunakan Gbr. 1.14
sebagai panduan, persamaan iteratif untuk gelombang maju dan mundur di sel B,
selama langkah (k + l), adalah
AXEL FERDIAN JAVAS WIDJAJANTO
TT KELAS 2C / 04
1731130016
MUCHAMAD BACHAQ NUDIN
TT KELAS 2C / 15
1730130130
ARIEF TRI KRISWINARTO
TT KELAS 2C / 02
1731130075